Adaptrade Software Newsletter Article

Tools for automated trading strategy development, such as Adaptrade Builder, are designed to create trading strategies with minimal user input and intervention. Instead of the trader coming up with the strategy idea and programming it, the user provides the overall requirements, and the software does the rest. This begs the question: how does a computer come up with trading ideas? The answer lies with the so-called variation operators.

If you've ever optimized the inputs to a trading strategy, you probably understand the basic idea of optimization. The goal is simple: you want to find the parameter values that maximize some objective, such as net profit or profit factor. The parameters for a trading strategy would typically be variables like indicator look-back lengths, so, for example, your goal might be to find the length of a moving average that maximizes the net profit of your trading strategy. While it might appear to be quite different, the same general approach is used with automated strategy development. Like finding the optimal input values for a trading strategy, automatically developing trading strategies is an optimization problem, and optimization depends on variation operators.

What do variation operators do? Optimization is essentially a systematic way of trying different values of the object being optimized until you find the value or values that maximize the objective function. For example, the simplest technique is to try every possible value and record the one that gives the optimal result. More sophisticated methods, such as genetic optimization¹ or particle swarm optimization,² as well as traditional methods, such as gradient descent³ or simulated annealing,⁴ provide different ways to select the values in order to arrive at the optimal solution faster, without having to try every possible value. The variation operator modifies the current value to arrive at the next value to try.

In a "brute force" optimization, in which every possible value is tried, the variation operator for finding the optimal look-back length would simply be to add 1 to the current value. In the steepest descent method, the variation operator involves the partial derivative of the objective function; it adds a fraction of the partial derivative to the current value so that it follows the slope of the objective function to its peak (or trough, depending on whether you're minimizing or maximizing). In general, the variation operators are what enable the search process to travel through the space of all possible solutions on the way to finding the optimal one.

When the object being optimized is a set of rules for a trading strategy, the variation operators need to be a bit more complex. In this case, the space of all possible solutions consists of all possible trading rules for the strategy. The variation operators need to be able to traverse this space. In other words, they need to be able to generate an endless variety of trading ideas. The variation operators are the idea generators of the optimization algorithm.

Evolutionary algorithms, such as genetic optimization and genetic programming, typically use two types of variation operators: crossover and mutation. These are the two basic types of variation operators used in Adaptrade Builder, as well as in other automated strategy development tools that are based on genetic programming. This article will illustrate the specific and unique variation operators used in Adaptrade Builder, as well as how several aspects of the evolutionary process are controlled.

Crossover and Mutation in Genetic Programming

When genetic programming is applied to automated trading strategy development, the strategy logic is represented by one or more tree structures. These rule trees evaluate to either true or false, which is used as a condition for either entering or exiting a trade. Crossover is a variation operator that exchanges a subtree from the rule tree of one strategy with a subtree from the rule tree of a different strategy. In this manner, two "parent" trees produce two "child" or offspring trees, as shown below in Fig. 1.

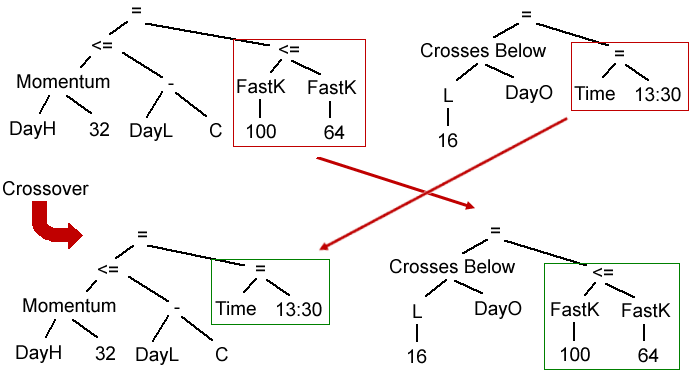
Figure 1. The crossover operator in Adaptrade Builder is used to swap part of one rule tree with another one. The two parent trees at top are equivalent to the following rules: (Momentum(DayH, 32) ≤ DayL - C) = (FastK(100) ≤ FastK(64)); (L[16] Crosses Below DayO) = (Time = 13:30). After exchanging the subtrees outlined in the red boxes, the new trees become: (Momentum(DayH, 32) ≤ DayL - C) = (Time = 13:30); (L[16] Crosses Below DayO) = (FastK(100) ≤ FastK(64)).

In the figure above, as with the figures that follow, the parent trees are shown at the top of the figure with the child trees below. The parts of the trees outlined in the red boxes are modified between the parent and child, with the modified parts outlined in green boxes on the child trees. In the case of crossover, the subtrees in the red boxes are interchanged. The indicator functions are abbreviated: O, H, L, and C represent the open, high, low, and close, respectively; DayH and DayL are the day's high and low prices, respectively, on intraday data; "=" is used to represent the equality operator (as opposed to "assignment"). All examples for this article are taken from actual build results from Adaptrade Builder.

The tree structure shows how the indicators are combined. For example, the tree in the upper-left corner of Fig. 1 can be written as (Momentum(DayH, 32) ≤ DayL - C) = (FastK(100) ≤ FastK(64)). The equality operator means that this expression would be true if the expressions on each side of the operator are either both true or both false at the same time. A key characteristic of crossover is that the basic components (i.e., indicators, operators, and input values) are not changed, but their arrangement is modified.

The mutation operators, on the other hand, change the basic components in one way or another. The simplest mutation operator is called point mutation, shown below in Fig. 2. In point mutation, the different components of the tree are changed with some mutation probability. For example, if the mutation probability is 20%, there's a 20% chance that a specific component will be changed. Each component is considered in turn, and if the randomly chosen probability is below the threshold, such as 20%, a new, compatible component will be chosen to replace the original one. "Compatible" means that the new component must not change the number of inputs or return type of any function, and, if it's a value, it must be within the same parameter range as the value it's replacing.

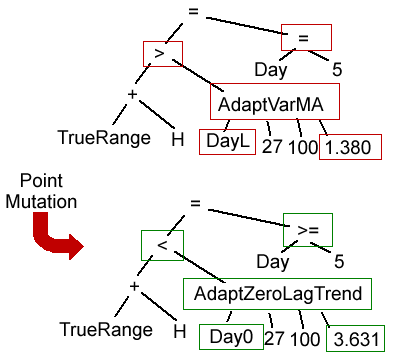
Figure 2. In point mutation, the components of the top tree in the red boxes are changed to similar components, shown in the lower tree in the green boxes. Before mutation: (TrueRange + H > AdaptVarMA(DayL, 27, 100, 1.380)) = (Day = 5). After mutation: (TrueRange + H < AdaptZeroLagTrend(DayO, 27, 100, 3.631)) = (Day ≥ 5).

In subtree substitution, also known as subtree mutation, a subtree is replaced by a new, randomly generated subtree. For example, in Fig. 3, below, the subtree shown in the red box is replaced by the new one shown in the green box.

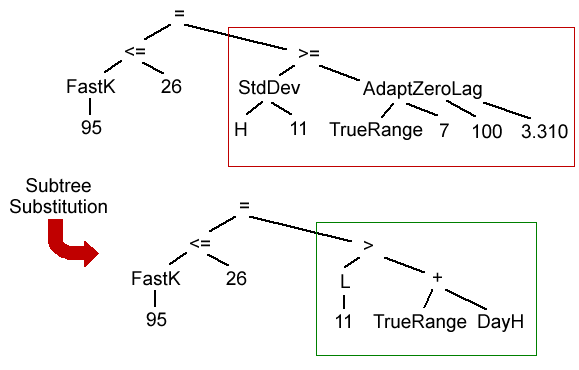
Figure 3. In subtree substitution, the child tree is created by replacing a subtree (shown in the red box) in the parent tree with a new, randomly generated subtree (shown in the green box). Before mutation: (FastK(95) ≤ 26) = (StdDev(H, 11) ≥ AdaptZeroLag(TrueRange, 7, 100, 3.310)). After mutation: (FastK(95) ≤ 26) = (L[11] > TrueRange + DayH).

Another way to mutate a rule tree is to make it more complex. The complicate operator performs this function by replacing a function with a small number of inputs with a more complex function that returns the same type of value, such as price, price difference, oscillator value, etc. An example is shown below in Fig. 4. In this example, the price function, O[13] (i.e., the open price 13 bars ago) is replaced by the 16-bar moving average of the open. The new function is chosen randomly from the set of all functions that meet the requirements. The complicate mutation operator not only retains the return type (price in this case) but the type of price (i.e., the open price).

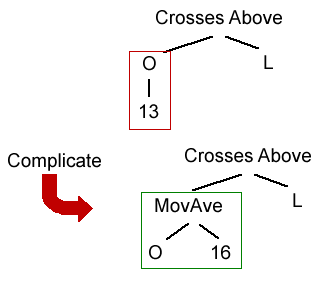
Figure 4. The complicate mutation operator replaces the function O[13] with the more complex function MovAve(O, 16), which retains both the return type (price) and the type of price (open). Before mutation: O[13] Crosses Above L. After mutation: MovAve(O, 16) Crosses Above L.

The opposite of the complicate operator is the simplify operator, which replaces a function with multiple inputs with a similar function with fewer inputs. The new function is chosen randomly from the set of all functions that return the same type but with fewer inputs. As with the complicate operator, the type of price (if applicable) is retained in the new function. For example, as shown in Fig. 5, the function WgtMA(O, 62) (i.e., 62-bar weighted moving average of the open) is replaced with the open price.

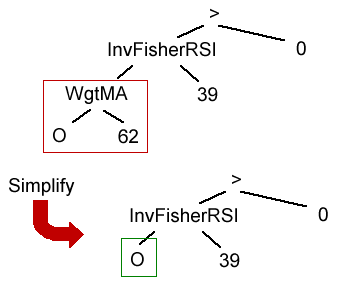
Figure 5. The simplify mutation operator replaces the function WgtMA(O, 62) with the simple price, O. Before mutation: InvFisherRSI(WgtMA(O, 62), 39) > 0. After mutation: InvFisherRSI(O, 39) > 0.

Another way to mutate a tree structure is to grow it. The subtree grow operator adds a new subtree to the existing tree. The new subtree is randomly generated and added to the existing tree using a new logical function, randomly chosen from "and", "or" or "=". For example, in Fig. 6, the new subtree "Time > 9:30" is connected to the existing tree using the "and" function. Both the complicate operator and the subtree grow operator increase the complexity of the tree, but complicate does so with minimal modifications to the tree structure, whereas grow always adds a new subtree.

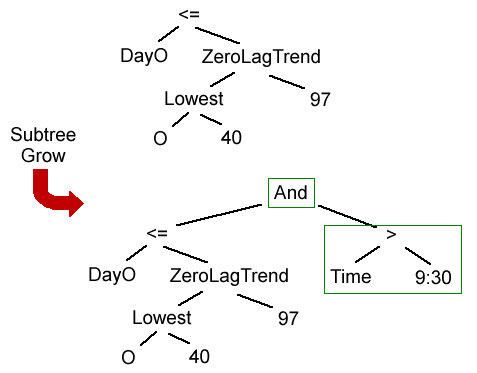
Figure 6. The subtree grow operator adds the new subtree Time > 9:30 to the parent tree using the "and" function. Before mutation: DayO ≤ ZeroLagTrend(Lowest(O, 40), 97). After mutation: (DayO ≤ ZeroLagTrend(Lowest(O, 40), 97)) And (Time > 9:30).

The opposite of growing a tree is pruning it. The subtree prune operator removes a subtree from the existing tree. The subtree to remove is randomly selected, and the parent logical function ("and", "or" or "=") is removed. For example, in Fig. 7, the subtree "H[14] ≤ DayL" is removed, along with the "or" function. Both the simplify operator and the subtree prune operator decrease the complexity of the tree, but simplify does so with minimal modifications to the tree structure, whereas prune always removes a subtree.

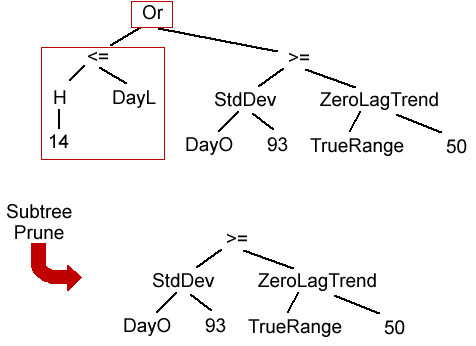
Figure 7. The subtree prune operator removes the subtree H[14] ≤ DayL from the parent tree, along with the "or" function. Before mutation: (H[14] ≤ DayL) Or (StdDev(DayO, 93) ≥ ZeroLagTrend(TrueRange, 50)). After mutation: StdDev(DayO, 93) ≥ ZeroLagTrend(TrueRange, 50).

Selecting the Variation Operator

The seven variation operators described above (crossover, point mutation, subtree substitution, complicate, simplify, subtree grow, subtree prune) are the way in which the genetic programming algorithm generates new trading strategies. However, with seven different ways to generate a new strategy, the algorithm needs to know which variation operator to choose. The first choice is between crossover and mutation. In Adaptrade Builder, the crossover probability, which is one of the user settings, determines the percentage of strategies generated via crossover, with the rest generated via mutation. For example, if the crossover percentage is 60%, that percentage of strategies will be generated via crossover with 40% generated via mutation.

Of the strategies generated via mutation, the mutation operator is chosen randomly according to the probability of each operator. These mutation probabilities are self-adaptive. That means that the probabilities of the six mutation operators are evolved along with the population of trading strategies. In other words, the same evolutionary process that's used to evolve the trading strategies is used to evolve the mutation probabilities. Each trading strategy has a set of mutation probabilities, and crossover and mutation are applied to the mutation probabilities during the build process. In doing so, the mutation probabilities associated with better strategies tend to be propagated to the next generation along with the strategies.

To see how this works in practice, consider Fig. 8, below. This shows how the six mutation probabilities, averaged over the population members, change during the build process. Initially, the six probabilities are initialized to random values near 16.67% (i.e., 100% divided by 6). The sum of the probabilities for the six operators must add up to 100%. Over successive generations, the evolutionary process tends to favor certain operators over others. In Fig. 8, the simplify operator has the highest probability, followed by point mutation and subtree substitution. At generation 600, for example, the probability of selecting the simplify operator was about 30%, the probability of selecting point mutation was about 25%, and so on (assuming mutation was chosen over crossover).

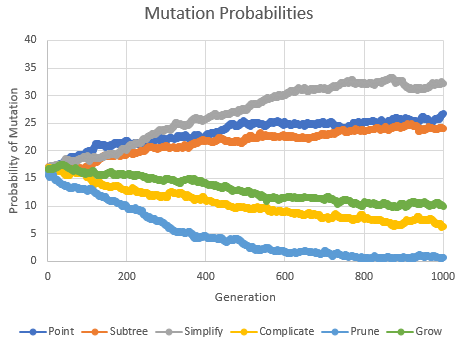
Figure 8. The probabilities of applying the six different mutation operators are evolved along with the population as part of the build process.

For other build examples, the probabilities will be different. Also, the ordering of the probabilities can change over time. For example, notice that in Fig. 8, prior to generation 200, the probability of point mutation was higher than that of the simplify operator. Also notice that the probability of subtree pruning tended towards zero after a large number of generations. This is probably because pruning is actively applied as part of a separate process to keep the tree depth from exceeding a specified limit. This is explained further in the next section.

Preventing Excessive Tree Depth

Each of the rule trees illustrated above has an associated tree depth, which is defined as the number of branches from the root to the end of the tree for the longest branch. For example, the parent tree in Fig. 7 has a tree depth of three, whereas the child tree in Fig. 6 has a tree depth of four. Tree depth is one measure of strategy complexity. Since high levels of complexity can increase the chances of over-fitting, Adaptrade Builder checks the tree depth of each strategy and applies the subtree pruning operator if the tree's depth exceeds the user's setting.

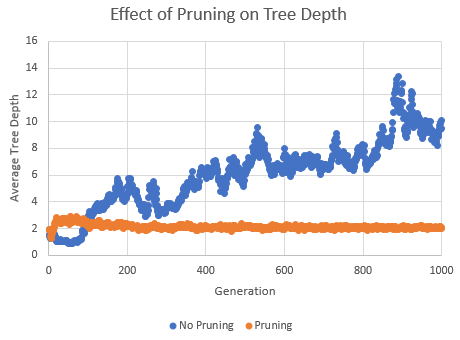
Figure 9. Without subtree pruning, the average tree depth tends to increase over successive generations. When subtree pruning is applied to strategies that exceed a specified tree depth, the tree depth remains nearly constant.

Over successive generations, this approach tends to keep the tree depth fairly constant, as shown by the lower curve in Fig. 9. Without this application of subtree pruning, the tree depth tends to increase, as shown by the upper curve in Fig. 9. Because the rule trees branch out further as the depth increases, a tree with a depth of six can have more than eight times as many "nodes" as a tree with a depth of three. Maintaining the tree depth during the build process via the subtree pruning operator is one way to prevent excessive complexity and over-fitting.

Conclusions

Automated strategy development using methods such as genetic programming can seem a bit mysterious at first. How does the software come up with trading rules and logic? How do the strategies evolve over successive generations? The variation operators described above are a key part of this process. The variation operators of crossover and mutation generate all new trading strategies after the initial population of strategies is established and enable the optimization algorithm to search the space of possible trading strategies in search of the ones that meet the user's objectives and requirements.

In addition to crossover, Adaptrade Builder uses six different mutation operators to provide for maximum variation in the strategy logic. If the user had to select the probabilities with which to apply all these different operators, it's unlikely the user would be able to choose the best probabilities for each build case. For that reason, Builder selects the mutation probabilities self-adaptively, which means they're evolved during the build process using the same evolutionary approach that's applied to the trading strategies themselves.

One potential drawback of employing a wide array of variation operators is that the complexity of the rule trees can increase over successive generations, potentially leading to over-fitting. To prevent this, the subtree pruning operator is applied to new strategies if their tree depths exceed the user's tree depth setting. This helps prevent runaway complexity while still allowing for variation. Complexity can still be independently controlled during the build process using the program's complexity metric, which is based on the number of independent strategy inputs. Since this is a different measure of complexity than tree depth, it's possible to achieve different levels of the complexity metric for the same tree depth limit.

References

1. Eiben, A. E. and Smith, J. E. Introduction to Evolutionary Computing, Springer-Verlag, Berlin, 2010, pp. 37-69.
2. Rini, D. P., Shamsuddin, S. M., and Yuhaniz, S. S. "Particle Swarm Optimization: Technique, System and Challenges", International Journal of Computer Applications, Vol 14, No. 1, pp. 19-27, 2011.
3. Gill, P. E., Murray, W., and Wright, M. H. Practical Optimization, Academic Press, Inc., London, 1981, pp. 99-105.
4. Michalewicz, Z. and Fogel, D. B. How to Solve It: Modern Heuristics, Springer-Verlag, Berlin, 2000, pp. 116-117.

Good luck with your trading.

Mike Bryant
Adaptrade Software