The Breakout
Bulletin
The following article was originally published in the June 2006 issue of
The Breakout Bulletin.
Dynamic Portfolio Selection
One of the side effects of
spending a lot of time studying and trading the markets is that you can end up
with a large number of trading systems. Sometimes, I'll develop a system and
forget about it for several months, only to find that it has performed better
during that time than the systems I've actually traded. Also, I can only trade
so many systems at once without losing focus and making mistakes, which means I
need to carefully choose the few systems I'll trade.
With
this in mind, I started to think about how to select the best market-systems
from among a larger set of available market-systems. By "market-system" I mean
the combination of a trading system and the market on which it trades. Since the
same system may trade more than one market, it's necessary to consider both the
system and the market, rather than just the system alone. It might appear that
the answer is simple: trade the best performing market-systems. If you have 10
market-systems, and three have been doing well lately, trade those three.
Simple.
In some
cases, that approach may work. However, that only works when those
market-systems have "positive dependency," which means that when they're
winning, they tend to keep winning. Many market-systems tend to be
mean-reverting, also known as having negative dependency, which means that if
they've been doing well recently, they're more likely to do poorly going
forward, and vice versa. Also, I want a method that works on short time frames.
Over a long period of time, it no doubt pays to drop losing systems in favor of
winning ones, but how do you choose the best market-systems for the next five or
10 trades?
The
method I came up with was motivated by my work with equity curve crossover
trading. Adding up a market-system's trades over times produces an equity curve.
If you fit a moving average through the equity curve, you'll find that the
equity curve for some market-systems tends to oscillate around the moving
average. When the equity is above the moving average, it tends to cross back
below it, and when it drops too far below the moving average, it tends to move
back towards the moving average. These are the mean-reverting market-systems.
With other market-systems, however, the equity curve can stay above or below the
moving average for extended periods of time. These are the market-systems that
tend to have positive trade dependency.
My
approach is to quantify the relationship between a market-system's past recent
performance and it's future performance, much like looking at the how the equity
curve moves relative to it's moving average. In particular, I calculate the
average trade profit/loss over the past NBack trades and then look forward to
calculate the average trade over the next NForw trades. For example, if NBack
and NForw are equal to 5, I'd calculate the average trade over the past five
trades and the average trade over the next five trades. Since, ultimately, we
want to know where to best allocate our money, I divide the average trades by
the margin requirement for one contract. (My examples are for futures, but the
method could be easily adapted to stocks.) The result is the average return
relative to margin for one trade.
Let's
say, for example, that the average trade return over the past five trades is
-10%, and the average trade return for the following five trades is +12%. This
implies negative dependency or reversion to the mean: following a losing period,
the market-system started winning. But the results for just one five-trade
average are not very meaningful, so we repeat the calculations for each trade in
the trade history and group the results into statistical "bins." For example,
over a history of 200 trades, there may be 15 trades where the average return
over the past five trades was between -20% and -10%. The average trade over the
next five trades in these 15 instances might average, say, +11%. This tells us
that if this market-system produces an average trade of between -20% and -10%,
we can expect an average trade following that of about 11%.
As an
example, consider the following two figures.
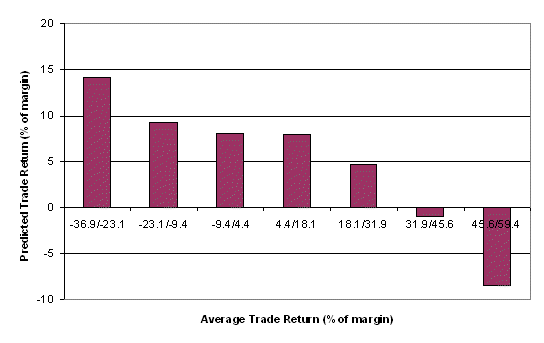
Figure 1. Predicted average
trade return based on the past average trade returns for the MiniMax system on
Yen (JY) futures.
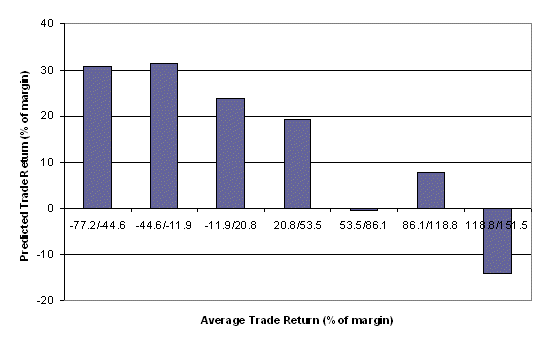
Figure 2. Predicted average
trade return based on the past average trade returns for the MiniMax system
on T-bond (US) futures.
These figures summarize this kind of
analysis for two different market-systems. In Fig. 1, the results represent the
MiniMax system traded on
Japanese Yen (JY) futures. The numbers under each bar represent the range of
average trade returns. The value of the bar (vertical axis) is the average
return over the next five trades. Fig. 2 presents the same results for the
MiniMax system on T-bond futures (US). For example, in Fig. 2, the left-most bar
is for average trade returns between -77% and -44%. When trade returns fall into
this range, the average trade return over the next five trades is about 30%.
Notice that the forward-looking trade return (predicted performance) tends to
decline as the average trade return increases. The worst predicted performance
occurs when the past average trade return is in the range 118% to 151%. This
implies reversion to the mean. Following poor performance, the performance tends
to be best, and after the best performance, the performance tends to be the
worst.
The results used to produce these
figures were generated using an EasyLanguage function for TradeStation that I
wrote called PredictedRoR. This function can be downloaded from my web site on
the free downloads page.
The function is called using the following format:
Value1 = PredictedRoR(5, 5, 10,
2000, "MiniMax", "C:\bcm\PredictedRoR-MiniMax.csv");
The first input is the look-back
length. The trades will be averaged over this number of trades; e.g., 5. The
second input is the look-forward length. This is the number of trades over which
the trade return will be averaged following the trades in the look-back period.
In Figs. 1 and 2, the look-back and look-forward lengths were both set to 5.
Input #3 is the approximate number of bins to group the data into. For example,
in Fig. 1 and 2, there are seven bins. If there are fewer than three data points
in any given bin, the function will reduce the number of bins and start again.
There must be enough trades to provide at least three bins (with a minimum of
three data points in each bin); otherwise, the function will fail. The fourth
input is the margin requirement for trading one contract. The next input is the
name of the system that calls the function, and the last input is the name of
the file to write the results to.
The function call, as shown above,
should be placed at the end of your TradeStation strategy code outside of all
loops and other program statements. The code collects the trade profit/loss
results on each bar, and, on the last bar of the chart, performs the
calculations and writes out the results to the specified file. The function
returns the predicted rate of return based on the current value of the average
trade return.
Here's an example of the output
generated by the function:
These are the results used to produce
Fig.2 above. The results include the current rate of return (-13.4% of margin in
this case) and the predicted rate of return (+31.5% of margin). The current rate
of return is the average trade return over the look-back period (5 trades in
this case) for the most recent closed trade. The predicted rate of return is the
predicted trade return (as a percentage of the margin requirement) based on
which bin the current rate of return falls into. In this case, the current rate
of return is -13.4%, which places it in bin #2. The predicted rate of return for
bin #2 is 31.5%, so this is the predicted rate of return over the next five
trades for this market-system.
The last section of the function
output displays the bins. The columns for the "Lower RoR" and "Upper RoR"
provide the range for each bin. The last column ("Predicted RoR") is the
predicted rate of return for the bin. For example, bin #4 is for returns between
20.8% and 53.5%. When the average trade return falls into this range, the
predicted rate of return is 19.3%.
One way to use this function is to
call it from each system you're tracking for possible inclusion in your trading
portfolio. After each closed trade, you would look at the predicted rate of
return, as output by the PredictedRoR function, and rank your market-systems
accordingly. If you have 20 market-system in total, and you want to trade the
top five, you would trade the five that have the highest predicted RoR.
Using my MiniMax system as an example,
here was the ranking at the time I did the analysis above:
Market System Predicted RoR
MiniMax-US 31.5
MiniMax-ER2 10.6
MiniMax-NK 8.0
MiniMax-JY 7.9
MiniMax-CL 7.2
According to this ranking, T-bonds
should do best over the next five trades, followed by the E-mini Russell 2000
and the Nikkei 225.
So does it work? Of the three trades
following the last closed trades used in the analysis, there was a trade in
T-bonds with an open profit of $1200 (86% of margin), a trade in the E-mini
Russell with an open profit of about $3200 (94% of margin), and a closed trade
in the Nikkei with a profit of $3700 (79% of margin). There have been no trades
in the Yen and crude oil since I did the analysis.
As with any method based on past trade
results, out-of-sample testing should be performed prior to risking real money.
That's all for
now. Good luck
with your trading.
Mike Bryant
Breakout Futures