The Analogy of System Optimization to Least Squares Regression

Last month I presented a simple statistical test based on confidence intervals to help evaluate the profitability of a trading system based on its trade history. One caveat to that test was that it can't tell us if the system has been over-fit to the market and therefore not likely to perform well in the future. This month, I'm going to try to address this problem by way of analogy to least squares regression.

Some traders believe the only good optimization is no optimization. Others re-optimize their systems every week. The wide diversity of opinions on the subject is reflective of the lack of concrete answers to the questions that system optimization raises. The primary question is whether optimization leads to systems that are "over-fit" to the market. Any profitable trading system is "fit" to the market in the sense that it must be aligned with some underlying characteristic of the market to be successful. I use the phrase "over-fit" to suggest that the degree of fit is so tight that if future market behavior deviates even slightly from the past, the system will become out of sync with the market and will not be profitable. From this point of view, the key to optimization is to fit the system to the market without over-fitting it. A system that is properly optimized will be able to handle normal variations in market behavior, whereas an over-fit system will not.

One way to understand the difference between fitting and over-fitting is to look at the process of system optimization as a kind of least squares regression; i.e., curve fitting. Consider the standard least squares curve fitting problem shown in Fig. 1. The problem is: determine the values m (slope) and b (y intercept) for the equation y = m*x + b that best fits the equation to the data points (x1, y1), (x2, y2), ..., (x5, y5). 

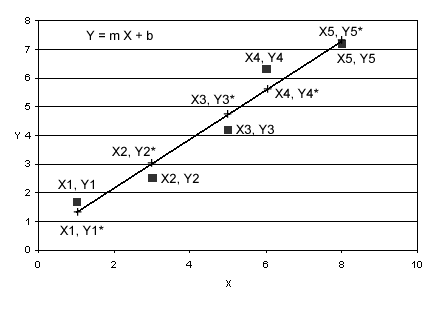
Figure 1. Fitting a straight line to a set of data points. The line is given by the equation y = m*x + b, where m is the slope and b is the y-intercept. The data points are given by (x1, y1), ..., (x5, y5). At the x value of each data point, the corresponding value of y that lies on the line is given by yi*; e.g., y1*, y2*, etc. The line is fit the to the data points by minimizing the sum of the squares of the differences between yi and yi*.
 

In the least squares method, we calculate the value of y that lies on the curve y = m*x + b at each data point, x (x1, x2, etc). For example, at x1, the y value of the curve is y1*. We then calculate the difference between the curve, y1*, and the data point, y1 and take the square of this difference. The sum of all such squares represents the total deviation of the curve from the data points. The values of m and b that minimize this sum give us the line that best fits the data points. This is the least squares regression method for fitting a line to a set of data points.

How is optimizing a trading system analogous to fitting a curve to a set of data points? With the linear equation, y = m*x + b, we plug in a value of x and get out a value y. The value y depends not only on x but on the form of the equation (linear in this case) and the equation's parameters, m and b. By analogy, with a trading system, we plug in a series of prices (we'll neglect volume and open interest for the sake of simplicity) and get out a profit or loss. The profit or loss depends not only on the prices but on the system's rules and parameter values. In this analogy, the system's rules are analogous to the equation fit to the points, and the system's parameters are analogous to the equation's parameters, m and b. The prices we feed into our system are analogous to the value x, and the resulting profit or loss is analogous to y. In other words, our system's trades are the data points (x, y).

The key to understanding how tightly an equation is fit to a set of data points or how tightly a trading system is fit to the price data is the "degrees-of-freedom (dof)." The number of dof is equal to the number of data points minus the number of restrictions or constraints. In linear least squares regression, the number of restrictions is equal to the number of adjustable parameters. For example, the linear equation above has two adjustable parameters, m and b. If we have two or fewer data points, we will have no dof. This would be the "tightest" fit possible, analogous to over-fitting a trading system. For example, if we have exactly two points, (x1, y1) and (x2, y2), we can determine m and b to exactly fit the data points. If we have more than two data points, we can determine m and b using the least squares method to minimize the deviation between the line and the data points. If we imagine the data points as being culled from a probability distribution of such points, then the more data points we include in our curve-fit, the better our curve-fit equation will represent that distribution. In other words, the more data points we use, the more robust our fit will be. In terms of dof, we want as many as possible.

We've already noted that the data points in system optimization are the system's trades. To make sure our system is not over fit to the market, then, we need to have a sufficient number of trades. By "sufficient" we mean more trades than the number of restrictions, conditions, and rules of our system. To count the number of restrictions, Thomas Hoffman (1) suggests scanning a trading system's rules and counting any condition that would change the resulting trades. For example, suppose you have a trading system that buys when today's close is less than yesterday's close in an up trend. It defines an up trend as when a shorter moving average is greater than a longer moving average. For simplicity, let's assume the sell side is the reverse, and there are no stops. It's a simple stop and reverse system.

We would probably count the moving average cross over condition as three restrictions, one for the condition itself, and one for each moving average period. The price pattern would be another restriction for a total of four restrictions for the long side. We would then count four more for the short side. This would give us eight restrictions in total. If we wanted to avoid over fitting this simple system to the market, we should have more than eight trades. With eight or fewer trades, there are no degrees of freedom, and any optimization is likely to result in an over fit system. The next question is: how many more trades than eight would be enough to avoid over fitting?

It turns out we can address this question using the same equation I presented last month; namely, the equation for the confidence interval for the average trade:

    CI =  t * SD/sqrt(N)

where t is the Student's t statistic, SD is the standard deviation of the trades, N is the number of trades, and sqrt represents "square root." The average trade is likely to lie between T - CI and T + CI. For the system to be profitable at our specified confidence level, we want the average trade, T, to be greater than zero at the lower bound, T - CI; i.e., 

    T > CI.

The part that I didn't explain last month involves the number of degrees of freedom. In last month's newsletter, I glossed over the choice of the t statistic, saying it was dependent on the number of trades and the confidence level. More precisely, t depends on the dof and confidence level. As long as the number of dof is large enough, the analysis I presented last month will work fine (although I incorrectly listed the confidence level for t =2 at 95%; it's actually 97.5% for a one-tailed test, such as we have here; see below). 

So, to see if our trading system is over fit to the market, we calculate the number of dof, look up the t statistic for our chosen confidence level and dof, and calculate the confidence interval as shown above. If the average trade is greater than CI, then we have some confidence that the system has a sufficient number of dof to avoid over fitting. When looking up the t statistic or calculating it with a function, such as the TINV function in Excel, use the one-tailed values since we are only concerned with whether the average trade is greater than zero.

Here are some t values to illustrate the idea:

        Confidence Level

dof     95%        99%

10     1.81        2.76

20     1.73        2.53

60     1.67        2.39

120   1.66        2.36

As an example, consider the simple system described above, which has eight conditions. Let's say the average trade is $250 with a standard deviation of $1000. If these numbers are based on a sample of 18 trades, then we have 18 - 8 = 10 dof. At 95% confidence, using the table above, the confidence interval is:

CI = 1.81 * 1000/sqrt(18)

    =  427.

So, we cannot say that the system will be profitable in this case, and any optimization -- no matter how good it looks -- is probably just over fitting the system to the trades. Even with 20 dof (i.e., 28 trades), you would find that the system does not pass this test at 95% confidence. However, if we have 68 trades and therefore 60 dof, we get:

CI = 1.67 * 1000/sqrt(68)

    = 203.

Since this value is less than the average trade of $250, we can have some confidence that if we were to optimize the parameters of this system, we would not over fit the system to the 68 trades in question.

For a long term trend following system, 68 trades might span 10 years or more of daily data, depending on the system. Whether the actual minimum number of trades is 68 or 30 or 200 depends on the average trade, the standard deviation of the average trade, and the number of rules and conditions of the system. Note that we're concerned with the number of trades and not the number of bars of data with this approach.

As I demonstrated last month, we can re-write the CI equation to tell us how large N needs to be in order to demonstrate profitability:
 

    N > (t * SD/T)^2
 

where the ^2 indicates "square." This assumes we have a good estimate for the standard deviation and average trade. This differs from the equation I presented last month in that t is explicitly included, rather than approximated. Again, t will depend on the number of dof, which depends on the number of conditions in the system and the number of trades. This means this equation must be solved iteratively, rather than explicitly, because t depends on N. For example, you could start with a small value of N, calculate the number of dof, look up t, calculate the right-hand side of the equation and see if it's less than N. If not, you increment N and try again. The first value of N that satisfies the equation tells you how large N needs to be.
 

As I mentioned last month, the primary concern with this approach is that the accuracy of the confidence intervals is dependent on the distribution of trades remaining the same. In statistics, this is called "stationarity." If the true average and standard deviation change over time, the confidence intervals will change. As all markets tend to change to some degree over time, this is a concern. However, even this problem can be mitigated to some extent by taking trades over a large period of time covering different market conditions. If this is done, the long term average trade and its standard deviation are more likely to be stable in the future.
 

Reference

(1) Babcock, Bruce. The Business One Irwin Guide to Trading Systems. Richard D. Irwin, Inc. 1989, p. 89.

That's all for now. Good luck with your trading.