|
 |
 |
| The Breakout
Bulletin
The following article was originally published in the November 2004 issue of
The Breakout Bulletin.
Better
Optimization in TradeStation
Optimizing a trading system is
a little like the way laws are passed in Congress. You may not like the process,
but it's probably better than having no laws at all. If your trading system
has one or more parameters, you have to choose values for those parameters,
whether or not you like the process of selecting them. Of course, you could
always pick numbers at random, throw darts at a calendar, or take the last two
digits of your social security number, but optimization usually (although not
always) seems like a more rationale approach. The well known drawback
of optimization is that too much optimization is not a good thing. If done
imprudently, optimization can curve-fit a trading system so tightly to the
market data used in the optimization that the system has no chance of
performing well on any other data. That kind of over-optimization has led many
trading pundits to reject optimization of any kind. In past issues of this
newsletter (see April and May, 2003), I've tried to show that optimization can
be perfectly acceptable provided it's performed over a sufficiently large sample
of trades. The more trades used in the optimization, the more likely it is that
the optimized system will hold up well in the future.
Of course, there are no free
lunches. When you optimize over a large samples of trades, it can be difficult
to find parameter values that work consistently well over all time periods and
market conditions in the sample. In particular, the optimization can
sometimes get "stuck" on one set of favorable market conditions, leaving
the system's performance elsewhere flat or poor. For example, when optimizing a
trading system for the stock indices, the optimal results may be unduly
influenced by the bubble market conditions that led up to the peak in early
2000. If you optimize for net profit, for example, you could end up with a
system that looks great in terms of net profit, profit factor, average trade,
drawdown, and most other summary statistics. But when you look at the equity
curve, you'd see that most of the profit was made from 1999 to early 2000 and
that the system was flat or down most other years. Another common problem is
when you can't find optimal results that give good recent performance, even
though the performance everywhere else in the past is good. Personally, I like
to use parameter values that have been doing well in recent trading. I'd
rather use parameter values that have been only OK in recent years but great in
recent trading than values that were great in past years but poor in recent
trading.
As an example, consider the
following equity curve for the Japanese Yen. This was produced by optimizing a
simple channel breakout system in TradeStation. The system has a single
parameter, the length of the channel. Based on optimizing for net profit, the
optimal channel length is 34 bars. Most of the equity curve looks great -- a
nearly straight line up to the peak. However, the first major peak is on
February 2000, followed by the second major peak on July 2002. Since then,
the system has been in a drawdown. If you had been trading this system, you
wouldn't have made any money since early 1998 and would be down
substantially since mid-2002. That's a long time to trade a system that isn't
doing well.
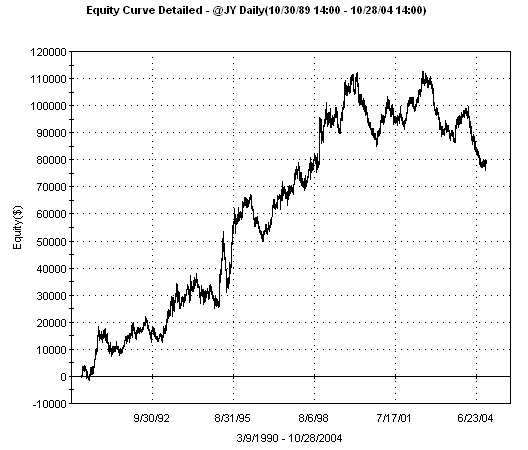
Fig. 1. Equity curve
for channel breakout system with a channel length of 34 bars, obtained by
optimizing for net profit.
The problem may be that this
type of system is inherently subject to big swings in equity. However, the fact
that it did consistently well for many years prior to 2000 calls that into
question. It may be that the Yen market has fundamentally changed, and the
system is no longer capable of performing well. However, it may also be that
using net profit as the optimization objective is too simple. The system did so
well for the first 10 years with one particular parameter value that even with
the poor performance in subsequent years, the net profit is still higher than
from any other parameter value. TradeStation lets you select other
performance measures for the optimization, but none of the other choices
gives better results in this case. The problem is that all the
optimization objective choices in TradeStation are simple summary
statistics.
In order to tell for sure
whether the problem is with the system or with the optimization, we need a
better optimization objective. Since we can't simply add
an optimization objective to TradeStation, I came up with
the following procedure to work around
the problem:
-
Implement an optimization
objective as an EasyLanguage function so that each time the system is run, the
objective function is computed. Have the function append the system input
values and the objective function value to a file, so that each time the
system is run, a line is added to the file.
-
Use TradeStation's built-in
optimization feature to iterate over different combinations of the system's
input parameters. For each set of parameter values, the function will add the
parameter values and objective function value to the file. There'll be one
line in the file for each set of parameter values.
-
Import the text file into a
spreadsheet and sort the rows according to the value of the objective
function. The row at the top will contain the optimal values of the input
parameters.
I'll illustrate this procedure
in a moment, but first we need an optimization objective. The problem with the
Yen system was that the optimization neglected the performance in recent years.
The result was that the equity curve tailed off at the end. One way to address
this is to look for parameter values that give a straight-line equity
curve. We would take the parameter values that produced the straightest,
upward sloping equity curve. We can quantify how straight a curve is using
the correlation coefficient. The correlation coefficient
measures the linearity ("straightness") of the relationship between the x and y
data of an x-y plot. The correlation coefficient is given by the following
equation:
R = [N
* Sum(Xi * Yi) - Sum(Xi) * Sum(Yi)]/sqrt[[N * Sum(Xi * Xi) - Sum(Xi)*Sum(Xi)] *
[N * Sum(Yi * Yi) - Sum(Yi)*Sum(Yi)]]
where N is the number of data
points, (Xi, Yi) is the ith data point, Sum() represents the summation of values
from i = 1 to i = N, and sqrt() is the square root. The correlation coefficient,
R, lies between -1 and +1. A R value of +1 means the relationship between x and
y is perfectly linear with a positive slope, which is what we want to see in our
equity curve. A value of zero means there is no correlation, and a value of -1
means the x and y values are negatively correlated.
To measure the correlation
coefficient for an equity curve, we can take Xi as the number of the ith bar,
and Yi as the total equity value (open plus closed trade equity) on the ith
bar.
Taking the correlation
coefficient as our sole objective function may be too simplistic. We could end
up with a straight equity curve but very low profitability. To avoid this, we
can add a term to the objective function to account for net profit. Our
objective function, which we'll want to maximize, will be a sum of the
correlation coefficient and the net profit. To make sure both terms contribute
equally to the optimization, we need to scale them so that each term is in the
range [0, 1]. Consider the following objective function:
OF = OW1 *
[(R - Rmin)/(Rmax - Rmin)] + OW2 * [(P - Pmin)/(Pmax -
Pmin)]
where Rmin is the minimum value
of the correlation coefficient over all optimization iterations, Rmax is the
maximum value of R, P is the net profit, Pmin is the minimum value of P over all
optimization iterations, Pmax is the maximum value of P, and OW1 and OW2 are
objective function weights. We won't know Rmin, Rmax, Pmin, and Pmax until we
run through the optimization once. We can then make a note of the maximum and
minimum values of R and P and use those to set Rmin, Rmax, Pmin, and Pmax for
the final optimization. The weights OW1 and OW2 allow us to give more emphasis
to either term. For example, if we want to emphasize straightness of the equity
curve over profitability, we could make OW1 larger than OW2.
Before putting this into
action, there's one other feature that can help with the optimization. Recall
that the problem with the Yen system was limited to the most recent part of the
equity curve. Another way to address this is to weight the most recent part of
the equity curve higher than the early part of the curve. Specifically, rather
than using the net profit, P, in the objective function, we could use a
"weighted" net profit. The weighted net profit can be computed as the weighted
sum of the equity changes from bar to bar, with the value of the weight
increasing from bar to bar, so that more recent bars have higher weights. To
increase the weight linearly, the following equation can be
used:
wi = (M -
1)/(N - 1) * (i - 1) + 1
where wi is the nonnormalized
weight for the ith bar, M is a factor that determines how much higher the weight
is on the last bar relative to the first bar, N is the number of bars (as
above), and i is the bar number. To keep the weighted net profit in the same
numeric range as the unweighted net profit, the weights, wi, should be
normalized as follows:
Wi =
wi/[Sum(wi)/N]
where Wi are the normalized
versions of the wi. The weighted net profit can then be computed as
follows:
PW = Sum(Wi
* Eqi)
where Eqi is the equity change
from bar i - 1 to bar i. Note that if M = 1, indicating that the weight is the
same on the last bar as on the first bar, then wi = 1 for all i, and Wi = 1 for
all i. The result is that the weighted net profit is equal to the net profit, PW
= P. So in the trivial case of no weighting, the equation for PW reduces down to
P as it should. To put more emphasis on the more recent part of the equity
curve, set M to a multiple of one; e.g., M = 10.
Using the weighted net profit,
the final version of our objective function can be written as
follows:
F = OW1 *
[(R - Rmin)/(Rmax - Rmin)] + OW2 * [(PW - PWmin)/(PWmax -
PWmin)]
where the weighted net profit,
PW, has been substituted for the net profit, P. In practice, since we've
normalized the weights for the net profit, the minimum and maximum values of PW
will be close to the minimum and maximum values of P, so Pmin and Pmax can be
used in place of PWmin and PWmax if you prefer. In fact, it's only necessary to
use approximate values for Rmin, Rmax, PWmin, and PWmax in any case since we can
always adjust things using the weighting factors.
Here's the EasyLanguage code
for a function that implements this objective function.
{
Function EqtyCorr
Calculate an objective function based on the
weighted sum of
the correlation coefficient of the equity curve and
the net profit.
Append the objective function value and system input
parameter
values to a file.
In the following, X represents the bar number, and Y is
the
total equity (closed trade net profit plus open position
profit).
Copyright 2004 Breakout
Futures
www.BreakoutFutures.com
}
input: Param1
(NumericSimple), { system parameter 1
}
Param2 (NumericSimple), { system
parameter 2 }
Param3 (NumericSimple), { system
parameter 3 }
Param4 (NumericSimple), { system
parameter 4 }
Param5 (NumericSimple), { system
parameter 5 }
CCMin (NumericSimple), {
min value of coeff }
CCMax (NumericSimple), {
max value of coeff }
EqMin (NumericSimple), {
min net profit }
EqMax (NumericSimple), {
max net profit }
WeightCC (NumericSimple), { weight for coeff
}
WeightEq
(NumericSimple), { weight for net profit
}
FName
(StringSimple); { file name to write results to
}
Var: XVal
(0), { value of x, scaled bar number
}
YVal
(0), { value of y, scaled equity
}
SumXY
(0), { sum of X * Y
}
SumX
(0), { sum of X
}
SumY
(0), { sum of Y
}
SumXX
(0), { sum of X * X
}
SumYY
(0), { sum of Y * Y
}
CCNum
(0), { numerator of correlation coefficient
}
CCDen
(0), { denominator of correlation coefficient
}
CorrCoef
(0), { correlation coefficient
}
ObjectFn
(0), { correlation times net profit
}
TotalEqty (0),
{ open plus closed trade equity }
TotProf (0), { total profit from weighted
sum }
PWNum
(0), { numerator of profit weights
}
PWDen
(0), { denominator of profit weights
}
PWFact
(100), { factor determining profit weighting
}
ii (0), { loop
counter }
NBars
(0), { number of bars on chart
}
StrOut
("");
Array: EqtyCh[5000](0); { handles up to 5000 bars
of data }
TotalEqty = NetProfit + OpenPositionProfit;
If
BarNumber < 5000 then
EqtyCh[BarNumber] = TotalEqty -
TotalEqty[1];
XVal = BarNumber/100.;
YVal =
TotalEqty/10000.;
SumX = SumX + XVal;
SumY = SumY +
YVal;
SumXY = SumXY + (XVal * YVal);
SumXX = SumXX + (XVal *
XVal);
SumYY = SumYY + (YVal * YVal);
{Print("Bar: ", BarNumber:0:0, " SumX = ",
SumX:0:0, " SumY = ", SumY:0:2, " SumXY = ",
SumXY:0:2,
" SumXX = ", SumXX:0:0, " SumYY = ", SumYY:0:2);
}
If LastBarOnchart then Begin
NBars = BarNumber;
{ Calculate weighted net profit
}
for ii = 1 to NBars
Begin
PWDen = PWDen + (PWFact -
1)/(NBars - 1) * (ii - 1) + 1;
End;
PWDen =
PWDen/NBars;
for ii = 1 to NBars
Begin
PWNum = (PWFact - 1)/(NBars
- 1) * (ii - 1) + 1;
TotProf =
TotProf + EqtyCh[ii] * PWNum/PWDen;
End;
{ Calculate correlation coefficient
}
CCNum = NBars * SumXY - (SumX *
SumY);
CCDen = SquareRoot((NBars * SumXX - (SumX *
SumX)) * (NBars * SumYY - (SumY * SumY)));
if CCDen
> 0 then
CorrCoef =
CCNum/CCDen
else
CorrCoef = 0;
{ Objective function is weighted sum of
profit plus correlation }
ObjectFn = WeightCC * (CorrCoef
- CCMin)/(CCMax - CCMin) +
WeightEq * (TotProf - EqMin)/(EqMax - EqMin);
{ write correlation coefficient to file
along with system parameters }
StrOut = NumtoStr(ObjectFn,
2) + ", " + NumtoStr(TotProf, 2) + ", " + NumtoStr(CorrCoef, 3) + ", " +
NumtoStr(Param1, 3) + ", " + NumtoStr(Param2, 3) + ", " +
NumtoStr(Param3, 3) + ", " +
NumtoStr(Param4, 3) + ", " + NumtoStr(Param5, 3) +
Newline;
FileAppend(FName,
StrOut);
End;
EqtyCorr = CorrCoef;
The first five inputs to the
function, Param1, Param2, ..., Param5, represent the input parameter values for
the system being optimized. Because it's difficult to optimize more than five
inputs simultaneously in TradeStation, I've limited the inputs to five. When
optimizing fewer than five, simply set the others to zero. If you do the
optimization in steps, a different output file can be used for each
optimization, and Param1 - Param5 can be set to different input parameter values
each time.
The inputs CCMin and CCMax are
the minimum and maximum values of the correlation coefficient, represented by
Rmin and Rmax in the equations above. The inputs EqMin and EqMax correspond to
the equation variables PWmax and PWmin above. Similarly, inputs WeightCC and
WeightEq correspond to OW1 and OW2 above. The multiplying factor that determines
how much more recent equity changes are weighted compared to earlier ones --
represented by variable M in the equations -- is given in the code by the
variable PWFact. This could be changed to a function input if you wanted to be
able to change it more readily.
To see how this function can be
used, the code below shows how it's called in the simple channel
breakout trading system I mentioned earlier, which was applied to the
Yen.
{
Simple Channel BO (breakout) system, based on
TradeStation systems
Channel Breakout LE and Channel Breakout
SE.
}
input:
Length(50);
Buy
("ChBrkLE") next bar at HighestFC(High, Length) + 1 point stop;
Sell Short
("ChBrkSE") next bar at LowestFC(Low, Length) - 1 point
stop;
Value1
= EqtyCorr(Length, 0, 0, 0, 0, .52, .945, 2400, 72000, 1, 10,
"C:\bcm\TestCC.txt");
The function is called in the
last line of the code. Because this system has only one input, the function
inputs Param2 - Param5 are set to zero. The next two function inputs are the
minimum and maximum values of the correlation coefficient. The next two are the
minimum and maximum values of the weighted net profit. Following those are the
weights for the correlation and net profit terms of the objective function,
respectively. Here, I'm weighting the profit term higher than the correlation
term. I'm doing this because I've set the net profit weighting factor
(PWFact in the code or variable M in the equations above) to a high value (100).
I'm hoping that by weighting the more recent part of the equity curve much
higher than the earlier part that the optimization will value parameter sets
higher that have high equity values at the end of the equity curve. If this
works, the optimal result should produce an equity curve that is profitable in
recent years, unlike the equity curve shown
above.
Let's see how it does. I
optimized the system shown above over input values (channel lengths) of 5 to 90
in increments of 1. This produced the output file TestCC.txt shown
below.
-7.17, -33322.26, -0.344,
5.000, 0.000, 0.000, 0.000, 0.000
1.55, 12573.79,
0.558, 6.000, 0.000, 0.000, 0.000, 0.000
5.30,
33526.75, 0.874, 7.000, 0.000, 0.000, 0.000,
0.000
-5.83, -24832.22, -0.296, 8.000, 0.000, 0.000,
0.000, 0.000
4.16, 26840.19, 0.797, 9.000, 0.000,
0.000, 0.000, 0.000
5.92, 38072.43, 0.857, 10.000,
0.000, 0.000, 0.000, 0.000
4.47, 30434.27, 0.707,
11.000, 0.000, 0.000, 0.000, 0.000
8.42, 54830.40,
0.895, 12.000, 0.000, 0.000, 0.000, 0.000
7.61,
48549.36, 0.936, 13.000, 0.000, 0.000, 0.000,
0.000
6.84, 43517.97, 0.915, 14.000, 0.000, 0.000,
0.000, 0.000
6.80, 42783.76, 0.945, 15.000, 0.000,
0.000, 0.000, 0.000
3.23, 19308.60, 0.861, 16.000,
0.000, 0.000, 0.000, 0.000
3.13, 18605.73, 0.862,
17.000, 0.000, 0.000, 0.000, 0.000
0.59, 2304.74,
0.775, 18.000, 0.000, 0.000, 0.000,
0.000
...
...
The first column is the value
of the objective function. The second column is the weighted net profit, the
third is the correlation coefficient, and the fourth is the input parameter --
channel length. The remaining columns are the unused system input parameter
values. I then opened this file in
Excel and sorted the results by the first column in descending order, which
produced the following table:
8.42
54830.4 0.895 12
0 0 0 0
7.61 48549.36
0.936 13 0 0 0 0
6.84
43517.97 0.915 14
0 0 0 0
6.8 42783.76 0.945
15 0 0 0 0
6.5 40627.96
0.949 26 0 0 0 0
6.5
40547.87 0.955 27
0 0 0 0
6.46 40398.79
0.945 28 0 0 0 0
6.02
37587.1 0.931 34
0 0 0 0
...
...
The highest
value of the objective function, 8.42, is on top. The corresponding value of the
channel length, 12, is our optimal channel length. The following chart shows the
equity curve for this system using the optimal channel length of 12.
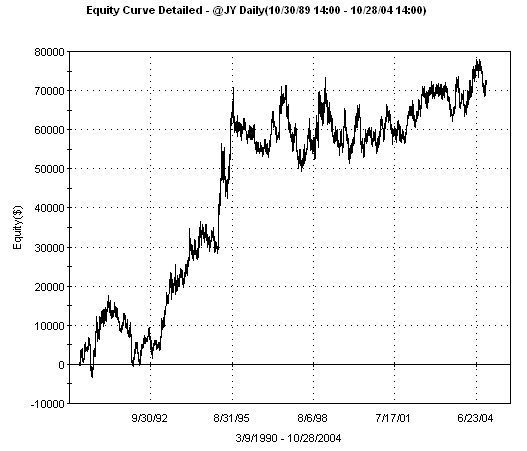
Fig. 2. Equity curve
for channel breakout system with a channel length of 12 bars, obtained by
optimizing the weighted net profit and correlation
coefficient.
Notice how the
equity curve is profitable in recent years (the peak is July 2004), unlike the
previous equity curve, which declined after a peak in 2002. The objective
function worked as intended. By weighting the equity changes higher in recent
years, the parameter value that produced the best results in recent years
produced the highest value of the objective function. And the equity curve
is still fairly straight overall because we included the term based on the
correlation coefficient.
Since we've
included the correlation coefficient in the output file, we can sort the data by
correlation coefficient (column C) to see which parameter value would
produce the straightest looking equity curve. Here's the file sorted by
correlation coefficient:
6.5
40547.87 0.955 27
0 0 0 0
6.5 40627.96 0.949
26 0 0 0 0
6.8 42783.76
0.945 15 0 0 0 0
6.46
40398.79 0.945 28
0 0 0 0
5.37 32835.54
0.944 29 0 0 0 0
7.61
48549.36 0.936 13
0 0 0 0
4.86 29413.79
0.935 23 0 0 0 0
3.68
21239.09 0.932 30
0 0 0 0
6.02 37587.1 0.931
34 0 0 0 0
...
...
The parameter
value that produces the highest correlation coefficient is 27. The
corresponding equity curve is shown below.
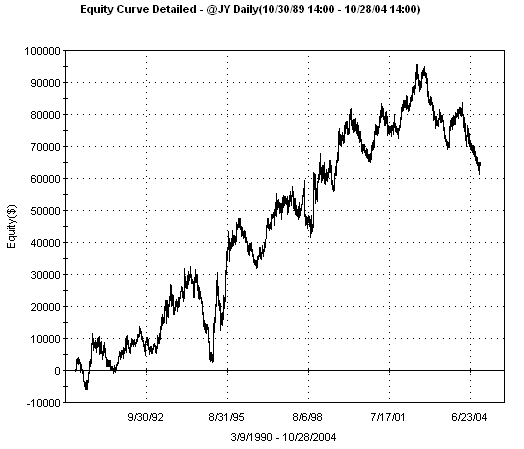
Fig. 2. Equity curve
for channel breakout system with a channel length of 27 bars, obtained by
optimizing the correlation coefficient.
Notice that the equity curve is
nearly a straight line -- aside from the usual wiggles -- up until the
peak, which occurs in July 2002. The system has been in a drawdown since the
peak using this parameter value, so optimizing based on correlation coefficient
alone doesn't solve the original problem of poor recent performance.
The EqtyCorr function can be
added to any TradeStation trading system to provide an alternative to the
optimization objectives available in TradeStation. Of course, just because the
equity curve is a straight line and the most recent part of the equity
curve is profitable is no guarantee that the system will be profitable going
forward. However, I'd rather trade a system like that than one in which the
equity curve has been in a protracted drawdown. As mentioned earlier, it's best
to optimize over as many trades as possible. The EqtyCorr function makes it
easier to find good results over a long sample of trades.
That's all for
now. Good luck with your trading.
Mike Bryant
Breakout Futures
|
|
 |